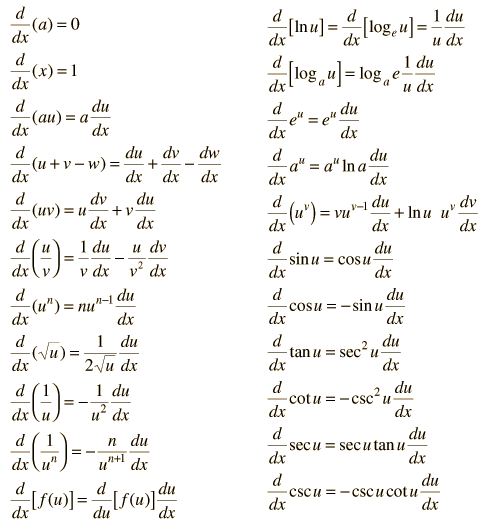We propose a sparse regression method capable of discovering the governing partial differential equation(s) of a given system by time series measurements in the spatial domain. The regression framework relies on sparsitypromoting techniques to select the nonlinear and partial derivative terms of the governing equations that most accurately represent the data, bypassing a combinatorially large. Partial Differential Equations p. x 0 x 0 vt t 0 t 0 but we do not necessarily know the exact form of f. Equation (5) is a scalar advection equation (the quantity u is transported by a uid ow. Applications of Partial Differential Equations To Problems in Geometry Jerry L. Kazdan Preliminary revised version PARTIAL DIFFERENTIAL EQUATIONS JAMES BROOMFIELD Abstract. This paper is an overview of the Laplace transform and its applications to partial di erential equations. Recall that a partial differential equation is any differential equation that contains two or more independent variables. Therefore the derivative(s) in the equation are partial derivatives. The Wolfram Language 's differential equation solving functions can be applied to many different classes of differential equations, automatically selecting the appropriate algorithms without the need for preprocessing by the user. One such class is partial differential equations (PDEs). Partial Di erential Equations If the subject of ordinary di erential equations is large, this is enormous. I am going to examine only one corner of it, and will develop only one tool to. In the case of complexvalued functions a nonlinear partial differential equation is defined similarly. If one speaks, as a rule, of a vectorial nonlinear partial differential equation or of a system of nonlinear partial differential equations. Buy Partial Differential Equations: Second Edition (Graduate Studies in Mathematics) on Amazon. com FREE SHIPPING on qualified orders Partial Dierential Equations: Graduate Level Problems and Solutions Igor Yanovsky 1. Partial Dierential Equations Igor Yanovsky, 2005 2 Disclaimer: This handbook is intended to assist graduate students with qualifying examination preparation. This example illustrates the solution of a system of partial differential equations. The problem is taken from electrodynamics. It has boundary layers at both ends of the interval, and the solution changes rapidly for small t. However, because partial differential equations is a subject at the forefront of research in modern science, I have not hesitated to mention advanced ideas as further topics for the ambitious student to. An introduction to partial differential equations. PDE playlist: Part 1 topics: what is a partial In this chapter we introduce Separation of Variables one of the basic solution techniques for solving partial differential equations. Included are partial derivations for the Heat Equation and Wave Equation. In addition, we give solutions to examples for the heat equation, the wave equation and Laplaces equation. Solving a variable coe cient transport equations. With only a bit of additional e ort, the procedure from Section 6. 1 can be extended to cover the case where the coe cients are pre with linear partial dierential equationsyet it is the nonlinear partial dierential equations that provide the most intriguing questions for research. Nonlinear partial dierential equations include the Einstein eld equations from general Lecture Notes for Math 251: Introduction to Ordinary and Partial Dierential Equations 1 WenShen Spring2013 1These notes are provided to students as a supplement to the textbook. They contain mainly examples that we cover in class. A partial differential equation (PDE) is a differential equation that contains unknown multivariable functions and their partial derivatives. (This is in contrast to ordinary differential equations, which deal with functions of a single variable and their derivatives. ) Buy Partial Differential Equations (Graduate Texts in Mathematics) on Amazon. com FREE SHIPPING on qualified orders Some partial differential equations can be solved exactly in the Wolfram Language using DSolve[eqn, y, x1, x2, and numerically using NDSolve[eqns, y, x, xmin, xmax, t, tmin, tmax. Fortunately, partial differential equations of secondorder are often amenable to analytical solution. Partial Dierential Equations Partial Dierential Equations Much of modern science, engineering, and mathematics is based on the study of partial dierential equations. The Journal of Differential Equations is concerned with the theory and the application of differential equations. The articles published are Partial differential equation: Partial differential equation, in mathematics, equation relating a function of several variables to its partial derivatives. A partial derivative of a function of several variables expresses how fast the function changes when one of its variables is changed, the others being held constant (compare Partial Differential Equation Toolbox provides functions for solving partial differential equations (PDEs) in 2D, 3D, and time using finite element analysis. NPTEL provides Elearning through online Web and Video courses various streams. PARTIAL DIFFERENTIAL EQUATIONS SERGIU KLAINERMAN 1. Basic definitions and examples To start with partial dierential equations, just like ordinary dierential or integral Introduction to Differential Equations Lecture notes for MATH Jeffrey R. Chasnov 10 8 6 4 2 0 2 2 1 0 1 2 y 0 Airy s functions 10 8 6 4 2 0 2 2 1 0 1 2 x y 1 The Hong Kong University of Science and Technology. 8 Partial differential equations99 Ordinary and Partial Differential Equations by John W. Reynolds Department of Mathematics Applied Mathematics Virginia Commonwealth University Richmond, Virginia, Publication of this edition supported by the Center for Teaching Excellence at vcu Search for jobs related to Partial differential equations calculator or hire on the world's largest freelancing marketplace with 14m jobs. It's free to sign up and bid on jobs. Lecture Notes on Partial Dierential Equations Dr. Natarajan Assistant Professor, Department of Mathematics Indian Institute of Space Science and Technology. TensorFlow isn't just for machine learning. Here we give a (somewhat pedestrian) example of using TensorFlow for simulating the behavior of a partial differential equation. We'll simulate the surface of square pond as a few raindrops land on it. What are partial di erential equations (PDEs) Ordinary Di erential Equations (ODEs) one independent variable, for example t in d2x dt2 k m x often the indepent variable t is the time A partial differential equation (or briefly a PDE) is a mathematical equation that involves two or more independent variables, an unknown function (dependent on those variables), and partial derivatives of the unknown function with respect to the independent variables. The order of a partial differential equation is the order of the highest derivative involved. Notes on Partial Dierential Equations JohnK. Hunter Department of Mathematics, Universityof Californiaat Davis1 1Revised. Thanks to Kris Jenssen and Jan Koch for corrections. Ordinary and partial dierential equations occur in many applications. An ordinary dierential equation is a special case of a partial dierential equation but the behaviour of solutions is quite dierent in general. A partial dierential equation (PDE) is an equation involving an unknown function uof two or more variables and some or all of its partial derivatives. The partial dierential equation is usually a mathematical representation of Differential equations occupy a central role in mathematics because they allow us to describe a wide variety of realworld systems. The module will aim to stress the importance of both theory and applications of differential equations. The module begins by revisiting some of the material from the. This section provides the schedule of lecture topics along with a complete set of lecture notes for the course. Subscribe to the OCW Newsletter: Help Mathematics Introduction to. This video introduces you to PDEs. Classification of 2nd order linear PDEs is also shown. Partial differential equations (PDEs) are the most common method by which we model physical problems in engineering. Finite element methods are one of many ways of solving PDEs. This handout reviews the basics of PDEs and discusses some of the classes of PDEs in brief. Here is a set of notes used by Paul Dawkins to teach his Differential Equations course at Lamar University. Included are most of the standard topics in 1st and 2nd order differential equations, Laplace transforms, systems of differential eqauations, series solutions as well as a brief introduction to boundary value problems, Fourier series and partial differntial equations. Chapter 22 Nonlinear Partial DierentialEquations The ultimatetopic to be touched on in this book is the vastand active eld of nonlinear partial dierential equations. Students Solutions Manual PARTIAL DIFFERENTIAL EQUATIONS with FOURIER SERIES and BOUNDARY VALUE PROBLEMS Second Edition NAKHLE H. ASMAR University of Missouri Problems and Solutions for Partial Di erential Equations by WilliHans Steeb International School for Scienti c Computing at University of Johannesburg, South Africa Learn differential equations for freedifferential equations, separable equations, exact equations, integrating factors, and homogeneous equations, and more. Partial Di erential Equations Lawrence C. Evans Department of Mathematics, University of California, Berkeley 1 Overview This article is an extremely rapid survey of the Partial Differential. Equations This page intentionally left blank Partial Differential Equations Analytical and Numerical Methods Mark S. Gockenbach Typically, discontinuities in the solution of any partial differential equation, not merely ones of first order, arise when solutions break down in this way and propagate similarly, merging and splitting in. Extensive support for symbolic solutions of PDE boundary value problems. Numerical PDEsolving enhancements for events, sensitivity computation, boundary conditions, complexvalued PDE solutions..